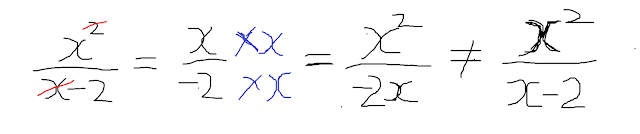Last week I had shared my classroom experience of working with students on polynomial division, and these students were not yet taught the standard procedure of solving such problems in their school. This is the link to the blog:
I forgot to mention one more interesting thing that happened while working on this problem, which I think would be worth sharing - esp for in-service maths teachers.
Before the two students (mentioned in the above / previous post) shared their solutions, another one had come up with this one :
Now, this mistake would not be new to the teachers who have been teaching algebra since long. Its one of the most common mistakes which would be done by at least one student in the class every year. I don't get irritated by these mistakes. I desperately wait for such mistakes. Yes ! Because I think it is a golden opportunity for the teacher if he / she is able to spot a student thinking / working this way. It presents just the right context and time for driving an enriching mathematical conversation in the whole class -- to know what other students think about this, if such misconception is simmering in someone else's mind too (& hence it would be nipped in the bud itself though the subsequent talk) and most importantly to know how my students see this / argue about this.
Do they say that --
a) This work is incorrect because it cannot be done this way. It is a rule! OR
b) Do they really reason about it, with proper math ?
When this student (S1) solve this way on the board, I was a little surprised as to why he did not 'cancel out' another 'x' too in the numerator (there was one in the term 3x too) and why he did not work with 10 and 2 in the same way? :)
I was about to argue (confuse) him by asking these, and when another student (S2) stood up - It is not possible to do this way.
On one side, I was a bit disappointed as he had foiled my plan (of confusing A), but on the other side, I was also happy that there was another student in the class who could spot some 'non-sense math' and object about it :) S1 was surprised by this remark of S2.
S2 went to the board and argued - How can we divide x^2 alone by x.... We have to first add the terms 3x - 10 to x^2 and then divide this sum by the expression in denominator.
Pause for a while and think what's your take on this argument.
---
While I was glad that he had noted and argued well about one aspect, I was not sure if he has missed or overlooked another important fact --- that it was not just a single 'x' term but a binomial 'x - 2' in the denominator (divisor). I was for sure going to delve into this matter in some time, but first I was curious to know how other students react to this argument of S2.
Almost all of them understood what he said, except couple of them. So he gave this example -
12 + 5
------------
3
12 / 3 = 4 . So can we say the answer of above expression is 4+5 = 9?
No, they replied. It is 17/ 3 which is 5 point something.....
And this was just enough to convince the ones who had not understood.
Wasn't this a fantastic creation? and that too made spontaneously ;)
--------
And now, it was my turn -- to play villain ;-))
Remember I stated my concerns above - I was not sure if S2 is also aware that S1's simplification was incorrect because of one more reason. (there is -2 sitting with x in the denominator)
So I asked them - But what if the question did not have more terms in the numerator? means, what if the question had just x^2 term.
I intentionally looked at S2 - Now, it would be okay to 'cancel out x' right ?
He was perplexed.... I was right when I was doubting about this part.... He had not considered this aspect yet...
But interestingly another student S3 jumped in and said - No ! We cannot do this.
Why?
Because we have to divide x^2 by (x-2) & in the above case, we are dividing x^2 by only x.
It is like -- The question is to divide 20 by (6-2) , and we are dividing 20 by 6 itself.... So the answer obtained will not be correct.
Fantastic !!
But I cannot give in so easily ;)
Is there any other way to prove that this is incorrect?
S2 bounced back. - 'Let us multiply the Numerator and Denominator of the answer by 'x' and see if we are getting the given fraction back.'
Since we are not getting the initial (given) fraction back, it means we have solved it wrong way.
He left me speechless. This thought deserved appreciation, isn't it?
But I responded to it with (an imp) finishing question - So will we ever be able to do this type of division?
Yes, we can do it - but only when there is no addition, subtraction in the numerator and denominator. Only when there is one term on both the sides. And while saying this, he happily showed did this on the board !
And the Devil in me had started cooking this type of situation now....
However, they had already gone into the celebration mood by now (winning against me), and so I thought to reserve this bouncer for the next match :)
-------
a] Do let me know your views / comments about this post. Would be glad to know 4m you...
b] And how would you respond / do you respond, when you see your students demonstrating such (common) algebraic misconceptions?
Thanks and Regards
PS: Students belong to class-7 marathi medium government school in navi-mumbai. I work with them voluntarily after their school hours as a part of maths enrichment program. www.supportmentor.weebly.com