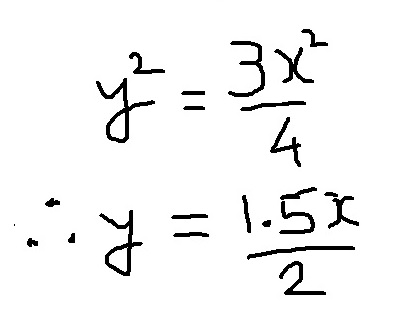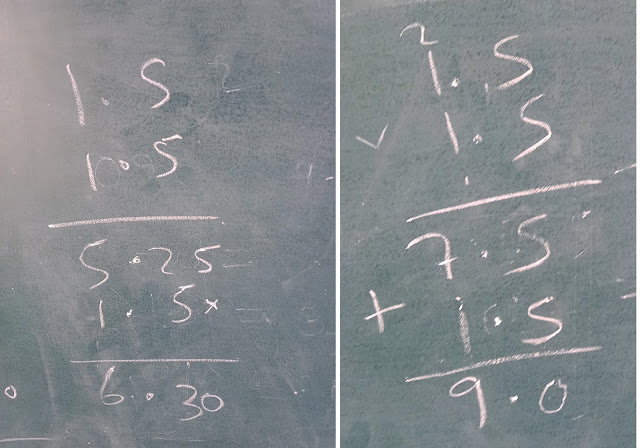Math Coach

Friday, January 31, 2025

Math-journey in the Train-journey ~ Part-2

I had observed that by now this 9-yr old was easily able to find out the results of subtraction problems where the first number is smaller than the second number. For eg: if we ask her what would be 7 minus 10, then she would say "Minus 3".

And how did such a young learner know about this Negative number thing? This interesting journey is shared in the Part-1 of this post... If you haven't read that yet, then it is recommended to read that Part-1 first before you read this Part-2... Here is the link:

https://rupeshgesota.blogspot.com/2025/01/math-journey-in-train-journey-part-1.html

So we continue our exploration further.

I draw her attention to the same previous problem 24-7 again.. I write these two numbers one below the other & write the digits of the answer after asking her:

- 7

---------

'four minus seven?"

She tells "Minus 3" and I write it down

"Two minus ...........Oh, what's the digit here before 7?", while pointing my finger to the blank space before 7.

She tells, "Its zero"

"Oh..okay"

i thought of asking her as to how does she know. But then chose to park this important question for later and go with the flow... So then I write zero before 7 and then ask her about the digit in the answer's place below 2 and 0.

She says, "Two" and I write it over there. (check image)

I now tell her, "So this answer is 17, right?"

And she looks at me with surprise.. and then comes her "No."

'Why? Didn't you find out some time back that 24 - 7 = 17?" while saying so, I showed her the previous work. (check image)

She looks at it. And then again looks at the strange looking new answer. But with no other response.

"So you say this newly worked out answer is not 17?"

"Yes..Its not 17"

"Then what's that number?"

"Umm... Its Minus 1"

'Oh.. and how is that -1?"

"Because 2 -3 equals -1"

"Oh..I get what you did..."

(Frankly, I was expecting this type of response from her... Did you also see it as -1, the way she did ? And did you also wonder about this strange looking answer?) :-)

I continue probing her..

'But then can there be two different answers for the same subtraction problem?"

"No"

"Then how come by previous method the answer is 17 and by this method, the answer is -1 ?"

No response..

"You want to know this?"

She nodded her head (implying yes).

So I draw her attention to the number 23 that was written somewhere on the ticket and ask her to read that number. She said Twenty three.

Now I write 312 on the ticket, and ask her to read it. She said Three hundred and twelve.

I ask her that both the numbers have digits 3 in it. What made her read them differently? (as in why just 3 in 1st case & as three hundred in 2nd case)

"In the first case, 3 is in one's place, and in Hundred's place in the second case"

I ask her that both the numbers have digits 2 in it. What made her read them differently? (as in why twenty in 1st case and just 2 in 2nd case)

"In the first case, 2 is in ten's place, and in One's place in the second case"

"Yes, so the place in which the digit is written decides its value. Right?"

'Yes"

Now I ask her - So what is this number Three hundred and twelve (312) made up of?

No response

"Whats the value of 3?"

"Three hundred"

"of 1?"

"Ten"

"of 2?"

"Two"

"So 312 is made up of ____?"

"300 + 10 + 2"

"Correct! remember you have studied this in your school.. Expanded form"

"Yes"

"So when we write 2 and 3 next to each other, how do you read it?"

"Twenty Three"

"But how did you get this value or name Twenty Three/"

"Twenty plus three"

"correct.. So twenty plus three equals twenty three."

I write 85 and ask her its value.

She says," 80 plus 5 equals eighty five"

I write 79 and ask her its name.

She says," 70 plus 9 equals seventy nine"

Now I again draw her attention to that strange looking answer of 24 - 7 which she had decoded as "Minus 1"

"So now with whatever we have learned / understood, can you find out what's the value / name of this number."

"twenty minus 3"

"Yes, how much is that/"

"Seventeen" but with a puzzled look and tone!

I saw that she was still not so satisfied with this seventeen. So I thought to show her the previous work which showed the familiar 17.

And then asked her if she remembered this?

"yes"

"Whats the answer of 24 minus 7 using old way?"

"seventeen"

Whats the answer of 24 minus 7 using new way?"

"seventeen" with some surprise & smile on her face...

"So both the answers are same?"

"yes"

"But then why were you unable to identify this strange looking number as 17 earlier?"

"because its not one seven seventeen, its two minus 3 seventeen"

"Hmm... its not one seven seventeen... Its ten plus seven seventeen"

"yes.."

"And here?"

"here its twenty minus three seventeen.... I have not seen such 17 in school / text book.. So I got confused."

"I get that... but you have understood this now?"

Smile on her face..

"Shall I give you one more problem?"

Quick and Joyful "yes"

So I tell her to solve 42-17. But first using the old/ school / textbook way, and then using the new way she has learned. And this is what she did.

As you can see from right side image above, she has also calculated the value of strange looking number as 25.

It was a delight to see Joy on her face & Confidence in her body language when she was able to verify that both the methods gave the same answer. (an experience that's rarely given to children in classrooms).

"One more?"

And there was 'yes" again!

"But this time I will be giving you a little difficult one...Okay?"

"Okay" she said while giving a smile to her mother sitting next to her ;)

I gave her 421 - 115, but with some change this time - first using the new way and then using the old way..... And this is what she did.

This time too, if you see the left image, she has calculated the value of the result: This is what she had done: 300 + 10 - 4 = 300 + 6 = 306

But she was disappointingly surprised when she got the different answer using the old way...

"Should we get both the answers same or different?"

"Same"

"But here both are different... So lets check both one by one properly?"

She did so. And could not find a mistake in any of those.!!

There could have been a better way to help her find out the mistake, but at that time I just told her to solve the problem again using the old way... And she did this....

There was a smile on her face as now, the two answers matched! And she also figured out the mistake in her previous work when I asked her to do so.... So I asked her -

"How come the mistake happened in the old method that you have been using since long and not in the new method that you have just learnt?"

She smiled at this...

"Which method do you like more?"

"New one"

"Really?"

"Yes"

"So when you go to your school, you will share this with your teacher and friends?"

"Yes"

I thanked her mother for being patient and allowing me to interact with her. And she thanked me for helping her child experience the Joy of Discovery..

Thanks & Regards

Rupesh Gesota

https://rupeshgesota.weebly.com

Math-journey in the Train-journey ~ Part-1

I often consider myself luckier -- to have at least one child near my seat during the long distance train travels..It not only kind-of shortens my journey but often such encounters / interactions have turned out to be enriching / interesting ones, and in many ways :-)

One such happened again recently. It was 13th Dec 2024, I was travelling by train to Ahmadabad from Mumbai. Just few minutes after I occupied my (window) seat, I saw a lady coming with an 8-9 yr old girl and occupying the seats in front of mine. I felt the Aha! within me, however 'controlled' my emotions for the time being :-)

After couple of hours, a girl, of age similar to that of the former one, came in our compartment to sell some key-chains. Soon she came to me and kept the tray full of key-chains on my lap suggesting me to take something. I thought for a while and then took one of those & put it in my pocket, giving her a smile. She kept looking at me with wonder for some time and then said, "Give me Rs.10"

"What for?"

"You took the key-chain."

"You gave me the tray and told me to take some.So I took."

"Give me Rs.10"

"Okay.. I will give. Tell me how much is this?" - while showing her 4 fingers,

"Four"

'Now?" - while showing 6 fingers,

"Six"

"Now?" - while showing 9 fingers,

"Seven.....No, Eight"

"Its not Eight."

She started counting one by one now... arriving at the correct answer 9.

"Good. Was there any other way?"

She thought for a while.. and then resorted to,"Give me Rs.10"

I removed the Rs.10 note from my wallet and while giving it to her asked her to show me her 10 fingers and she did so... Now, I just closed one of her fingers and asked her to tell this number.... And she said, "Nine"

"So was there another method?"

She shook her head (implying yes) and left with a smile and the 10 rupee note...

And I saw that this game (between me and this girl) had drawn the attention of some passengers around, including that of the girl sitting in front of me. I smiled at her and she shyfully pushed herself into her mom trying to hide her face :-)

Later, I noticed that her mother was telling her to sleep but she didn't want to.

"May be she has already slept for 20 hours!" I said this while looking at her.

She shook her head (implying no) with a smile...

"Oh.. you don't sleep much? How many hours do you sleep then --- 2 hrs, 3 hrs?"

"More than that..".

Phew!! finally she spoke! ;-)

"Oh okay... What time do you sleep?"

She looked at her mom for the answer who told her "around 11 o' clock"

"And you get up at?"

Again she looked at her mom for the answer -- "6 o' clock"

"Hmm... So how long do you sleep then?"

I see her thinking and then it comes from her -- "Seven hours"

"Yes...correct.. so then how many hours are you awake?"

She gave me a puzzled look...

"Why? Is it difficult to find?"

No response for few seconds..

"Do you know how many hours in a day?"

"24 hrs."

"So can you find now?"

I see a smile on her face and her fingers start moving in the air now.. :-)

"18 hrs." she said.

"What???" her mother reacted loudly to this (wrong answer!)..And I had to request her to hold / hide her reactions for a while..... Luckily, she understood and kindly stayed away from the rest of the game, though she paid attention to our conversations probably to learn something from this....

I asked the girl how did she calculate 18 hrs... Her explanation implied the vertical orientation of numbers - (standard) subtraction algorithm.

"Hmm OK.. Do you have pen and paper?"

"No"

The passenger next to me who was listening to all this kindly & immediately offered his pen and one of the old train tickets from my wallet became our note-pad.

"Can you plz show your work on this paper?"

And this is what she did (check image)

She was surprised with this answer, as it was different than the one she had said.

She gave the paper back to me with a shy smile.

"So how many hours do you sleep?" :-)

"17 hrs." with a smile & pinch of embarrassment.

I decide to play devil now... "I think there is some mistake in this work. . Let me show you where.".... And I scribble the numbers on paper while trying to explain that 4 minus 7 equals 3 and then 2 comes down as it is. . So the answer is 23. (check image)

And then she gave me a strange look while shouting -- "No, its wrong"

"Whats wrong? Isn't 7-4 equals 3?"

"It is.. but here it is 4-7"

"So?"

"That's not possible... So we borrow from 2."

"Oh okay.. I got it..."

She looks relieved now :)

"But you know what? you said that 4-7 is not possible... But actually, its possible!"

Again a strange look :-)

"You want to see?"

Curiosity is high by now!!

"Take your mom's phone.. Do you know calculator?"

She takes her phone, starts the App and waits for me.

"See what happens when you type 4-7 in it"

And guess what -- it happened what was expected -- puzzled look on her face again! And I could see her mother hiding her laughter :-)

"What's the answer?"

She said "3"

"Ummm.. its not 3.... Plz read properly"

She looked down and with little hesitation came..... "Minus 3"

"Yes,. 4 - 7 is minus 3....So its possible or not?"

She was smiling but I could also see some dissatisfaction on her face.

"What do you think 8-10 is possible?"

"No"

I was surprised by this. But then told her "Lets check on the calculator."

And soon came "Minus 2" with a surprised smile from her...

"So now what do you think, will 10-40 be possible?"

She was about to plug these symbols on the calci and I stopped her!!

"Wait... I want you to guess first now.. What would be the answer?"

And within couple of seconds she said "Minus 30"

"lets check this on calci now"

And when HER Answer appeared on calci, Joy too appeared on her face!

I saw there was a smile on mother's face too :)

We played this game with few more pairs, like 40-90, 30-25, etc in the Same order - first Guess & then Check. It was a delight to see her play & enjoy this (new) math!

Well, if you think that the game was over... then the answer is NO! . Something more was simmering in the teacher's mind... in fact, the real game was about to begin :-)

And you might wonder what's that? This adventurous journey is shared in the Part-2 of this post... Link below :-)

https://rupeshgesota.blogspot.com/2025/01/math-journey-in-train-journey-part-2.html

Thanks and Regards

Rupesh Gesota

https://rupeshgesota.weebly.com

Thursday, February 9, 2023

What's the value of Square-root of 3? - Part-2

So they come on the 2nd day, and I ask them -

"Could you find the value of Square root of 3?"

People who have not yet read the previous part of this post (Part-1), then it is suggested to read that first, so as to get the context of how we landed up here and what are the mistakes, conversations & learnings that happened in that process. Here is the link

http://rupeshgesota.blogspot.com/2023/02/whats-value-of-square-root-of-3-part-1.html

"Could you find the value of Square root of 3?"

"We tried.. But we didn't get"

Means?

"1.73 squared gives less than 3 and 1.74 squared gives more than 3."

I was glad that they worked with numbers having 2 digits after the decimal point, rather than just stopping at 1.7 and 1.8. But then I also wondered how come they didn't go beyond that. So I asked them -

"So what does that mean?"

"It means, value of root 3 is between 1.73 and 1.74"

"And how do you find that now?"

Puzzled look.

------

I told them to enlist the numbers they tried for the very first time... they wrote

1.6

1.7

1.8

1.9

"Then what did you do?"

"We understood that its between 1.7 and 1.8 and hence tried the numbers from 1.71 onwards...

"Okay.. So plz enlist these numbers too in the second column..."

1.6 1.71

1.7 1.72

1.8 1.73

1.9 1.74

They stopped at 1.74, saying they did not try beyond this as 1.74 squared crossed 3... I agreed but asked them to continue enlisting beyond 1.74 & they wrote till 1.80.

Can you guess what might be the teacher planning for?

...

1.6 1.71

1.7 1.72

1.8 1.73

1.9 1.74

1.75

1.76

1.77

1.78

1.79

1.80

"So Now?"

"We don't know what to do now..."

After a while, I drew their attention to the shorter first column & told them to complete this list too - write the numbers above 1.6.... They wrote till 1.1

1.1

1.2

1.3

1.4

1.5

1.6 1.71

1.7 1.72

1.8 1.73

1.9 1.74

1.75

1.76

1.77

1.78

1.79

1.80

"So these numbers are between ?"

"1 and 2"

"How did you get these numbers between 1 and 2?"

"By dividing the range into 10 parts"

"Ok.. And how did you get the numbers 1.71, 1.72, 1.73 etc.? I am asking this because I don't see these numbers in the first column?

"We knew its between 1.7 & 1.8 So we divided the range 1 to 2 into 100 parts now"

I circled around the numbers 1.7 and 1.8 when they said this and told them -

"So can we say this second column is kind of Zoomed-In-picture between 1.7 and 1.8? ... numbers which were present but not visible earlier have become visible now because you have divided the range into smaller i.e more (100) parts.. Its like you have kept a magnifying glass now on the two numbers 1.7 and 1.8", and while pointing my finger from the circled part of 1.7 and 1.8 towards the second column.

I paused a while to help them understand this new analogy being presented.

Share you thoughts after reflecting on what you read above...

...

"So now you say that the answer (the number) is between 1.73 and 1.74. What can we do now?"

They said - "We will divide the range further - into 1000 parts now - so that the numbers between 1.73 and 1.74 become visible" while saying this the student also circled around the pair 1.73 and 1.74

They started enlisting from 1.731, 1.732 and so on till 1.740. So I asked them what does 1.740 represent. They said its same as 1.74.

So then I told them to include another form of 1.73 too because they have circled / zoomed this number too.. Was this intervention / step needed ? why?

So in that column, he wrote 1.730 above 1.731

How about completing the first column too this way?

He checked and wrote 1.70 above 1.71

Now I drew their attention to the two circled pairs and the list of numbers next to each pair. So that they can also actually / easily see (& not just visualise) that

(1.7, 1.8) expands to range of numbers from (1.70 to 1.80) next to it, and

(1.73, 1.74) expands to range of numbers from (1.730 to 1.740) next to it.

The picture started looking like this in some time....

The squares of 1.731, 1.732 and 1.733 were calculated by them manually using std. method, but when it came to testing the squares of numbers in other columns (one with 4 and more digits after the DP), then I became their assistant and helped them getting & giving the squares of numbers which they wanted, with the help of my phone calculator.

Share your thoughts about the above paragraph (practice(s) employed by the teacher in this approach).

...

....

...

Things had gone into auto-pilot mode now and they were sort of thrilled / enjoying this process, totally surprised as this hunting never seemed to stop, against their expectation...... They said that they had never thought that square root of a number (that too such a smaller one like 3) will have so many digits :-))

I also shared with them that they don't need to enlist all the numbers in a column but can use dotted lines to indicate that.... Share why the teacher must have done so?

After some time, I stopped them and asked them what do they think about this process ?

"Sir, it seems this is never going to stop.... We are just reaching closer and closer to the answer...."

And how do you know this? (Note this question instead of validation from teacher)

"Square comes out to be 2.9999.... or 3.0000..... and few other digits are also there after 9 and 0 .... And then number of 9's and 0's keep increasing...."

So what would You do at this moment?

...

....

...

I asked them if they can be very sure of at least some digits in the square root of 3?

They looked for a while in all the columns and noticed the growing & unchanging section of digits. As you can see above , they have written the value of square root of 3 as 1.73205_......

I asked them if some one tells square root of 3 equals 1.732 then is it correct?

They said - "No.. Answer is closer to 1.732, but not equal to 1.732"

Share your thoughts about this response coming from students..

...

Looking at their facial expressions and body language, It was clear that this exercise was no less than an adventure ride for them :-))

So now it was Time to plug-in this correct value of root-3 into the expression they had arrived at (remember the previous post? :)

'x' and 'y' in the above equations represent the respective lengths of hypotenuse and side opposite to angle measuring 60 degrees in the Right Angled Triangle...

They were told to construct two Right Triangles (with angles and hypotenuse lengths given) and they had then measured the lengths of other two sides in both triangles..... They had observed the relation between hypotenuse and side opp. to angle measuring 30 and next job was to find the relation between hypotenuse and side opposite to angle 60.....

They were delighted to see that their measured lengths "almost matched" the lengths given by the formula.... Further, the value of Square root 3 was also figured out by themselves....

They asked why the measured lengths did not exactly match the calculated lengths...

So we discussed about how to round-off a decimal number at this moment -- that too based on understanding and not by rule, as can be seen in above two images... We also talked about construction/ measurement error, resolution of measuring devices. etc.

"Now we know why Square root 3 is written as it is in text-books!" , they exclaimed.

So what about square root 2 ? -- I asked them.

share your thoughts about asking this question at this moment..

...

....

They thought for a second and understood there can be list of such numbers like square root of 5, square root of 7, etc.., and I concluded this discussion saying that such numbers are called as Irrational numbers (of course with this thought in mind that this definition / explanation is not yet so precise and complete yet)

We moved to other topic, while giving them this assignment to find the value of square root of 2 (another irrational number which appears much in school mathematics) and they happily agreed to find out its value..

Thanks and Regards

Rupesh Gesota

www.rupeshgesota.weebly.com

Wednesday, February 8, 2023

What's the value of Square-root of 3? - Part-1

Plan was to help them see the relationships between the side lengths in 30-60-90 Triangles. But without hinting this to them, I told them to Construct couple of Right angled triangles in their note-books having other angles as 30 and 60 and with lengths of their hypotenuse as 10 cm and 6 cm

Then I told them to measure & tell me the other 4 side lengths in both triangles. I wrote these on the board as above and then asked them - What do they Notice? They were quick to see and say that

"in both the triangles, the shortest side length is always half the longest one"

I told them to construct two more Right Triangles, with hypotenuse as some whole numbers, but with angles other than 30 & 60 this time. They observed that in these cases shortest is Not half of the longest. So they said this relation holds true only when the angles are 30-60-90. (Can the need & timing of this 2nd activity be justified?)

So now I drew the following figure on the board and asked them if they could find which side length would be half of the hypotenuse length, without actually constructing it. (what could be the reason for doing this activity? Isn't this a mere repetition of the very first activity?)

Now It took some time for them to figure out. But after carefully studying previous figures, they said that "Side opp. to 30 degrees will be half of the hypotenuse"

So now, I asked them - If there could be any relation between the side opp. to 60 degrees angle and hypotenuse?

Their side lengths were in decimals (5.1 and 8.7), so it was naturally difficult for them to easily relate those to hypotenuse lengths. I asked them if they know any theorem that can be used in Right Angled Triangles. And they immediately said - Pythagoras theorem. And so we applied it & finally reached till this step.

Only last part of the derivation is showed above. A right angled Triangle was drawn where Hypotenuse was 'x', side opp. to 30 degrees angle = x/2 and side opposite to 60 degrees angle was shown as 'y'. Each of these steps were told by them and just written by me. I asked them how did they arrive at (1.5 x / 2) and they said

"Square root of x^2 = x , square root of 4 is 2 and sq. root of 3 is 1.5"

Suggesting you to Pause and think how would you respond at this moment?

...

"Okay... And how do you know that sq. root of 3 is 1.5?"

"Sq. roots of 1 and 4 are 1 and 2 resp. So sq. root of 3 has to be between 1 and 2.. So it should be 1.5"

Before reading further, I suggest you to pause and think for a while as to what would you do at this moment ?

...

I asked them if they can verify it. They started multiplying 1.5 by 1.5 using standard procedure. I would have loved seeing them figure out this product mentally through reasoning (Can YOU try that way before reading further?) And I thought we will discuss this approach once they get the answer using std. method, but then something else happened (& now I was in fact glad that they went by the std. multiplying method :-)

They seemed puzzled / uncomfortable with their results. So I told them to show their work on the board.

"What's the problem?"

"Both answers are incorrect as they are greater than 4. Because the product : 1.5 times 1.5 has to be between 1 and 4."

"Okay... But then how come both of you have got different results?"

So then they started comparing / studying each other's methods. And one of them tried this:

"But then this is also incorrect. It is less than 1", he said

Pause a while to study their 3 multiplications.. How will you categorise these mistakes? What could be the reasons for each of these?

"Okay... So what to do now? How to find what's 1.5 x 1.5?" I asked. They looked more engaged / puzzled than earlier now. I waited for about half a minute. After that, I decided to intervene. (Share your comments about this paragraph (approach by the teacher)

And before reading further, I suggest you to pause and think for a while as to what would you do at this moment ?

....

.....

....

There can be many ways. This is what happened through me at that moment:

"What's the other way we can write 0.5?" (when can a teacher help by asking such a question?)

And they picked up the hint and did this:

They reasoned out for 6/4 as if 6 chapatis given to 4 people, then each gets one and half, so 6/4 = 1.5 and 1/4 = 0.25 because 1 rupee = 100 paise, so quarter means 25 paise.

They were delighted with this answer 2.25 because it satisfied their expectation that it needs to be between 1 and 4. Further the boy who had worked out 1.5 x 1.5 as 0.225 on the board, something clicked to him; he went and corrected his answer -

"I had placed the decimal point incorrectly"

"But then how would you know where to place the decimal point?"

He studied the work again, and said, "Count the number of digits after the decimal point in both the numbers, add them, & then place it accordingly in the product."

"Okay.. It seems you have made a Rule. Will this always work?"

"Sir let's take one more example." And they did this:

"Okay... but what if there is 1 digit after the dp in 1st no. and 2 digits after the dp in 2nd no. ?"

"Then we will put the dp after 3 digits in the product."

"Will that work?"

"We will take an example to check." And they did this :

((( I would like to share something interesting that happened when they were framing the example for this case... One of them selected the numbers as 11.5 and 1.5 Why do you think he took such numbers?

I would have loved to see the story that can unfold after testing with 11.5 and 1.5, but since both of them were working together, so the other boy noticed this and he corrected him explaining what rule they are testing... Later I felt, I could have even suggested this boy to continue his testing independently with 11.5 & 1.5 .... )))

So now they were stuck with another problem: How to write 7/8 in decimal form?

They had been using 1 rupee = 100 paise, 1/2 rupee as 0.5 and 1/4 = 0.25 till now. So now they were struggling for 7/8.... For a while, they suggested 0.12.5 for 1/8 (Can you reason out why they must have said so?) But then they said they were uncomfortable with this because they had never seen such notation till now. After a while, they got stabilised at following:

They noticed that the digits (8,7 and 5) in this new representation were same as the ones they had got by multiplying 1.5 and 1.25 using standard method. But the different positions of decimal points in these two representations was bothering them.

Suggesting you to Pause here and Think about your approach now..

...

"Okay, so you have been dividing the whole into 100 parts to find the digits after the decimal point, right?"

"Yes.. because 1 rupee = 100 paise"

"Do these numbers represent always Money?"

"No"

But this hint did not help them... They were still stuck...

Suggesting you to Pause here & Think about your approach at this moment...

...

"How do you write half?"

1/2

"And using decimal point ?"

0.5

"How do you get this 5 in 0.5? Why not 0.2 , 0.3 ?"

We can write 1/2 as 5/10 and Out of 10 parts, we have taken 5 parts... So 0.5

"Okay... So you have converted 1/2 into other form 5/10 to find the decimal point form of half ? "

Yes

"But then why not write 1/2 as 3/6 and then write half as 0.3 ? Or write 1/2 as 4/8 and write half as 0.4 ?"

No answer. Puzzled.

"You have been dividing the whole into 100 parts till now to get the digits after the decimal point... So how will you write half in such case ?"

They said : 50/100 which is 0.50

"So do 0.5 and 0.50 both mean half ? "

Yes

"Which one is greater?"

Both are equal. 5/ 10 can be written as 50/100

"What about 0.500 ?"

This is also same ... Here we have done 500/1000

I thought this discussion might help them to think, go back and divide their whole into 1000 parts now instead of 100 which they had done because of which they had got decimal point number in the Numerator (87.5) and they felt stuck... But probably this much discussion didn't click much to them either... So then I asked -

"How do you write 1/4 using decimal point ?"

0.25

"How do you get this ?"

25/100

"Can we divide here too into 10 parts as we had done with half ?"

Yes. It would then be 2.5 / 10

"So which of these mean quarter ?"

All of these.

So I now wrote all of these in a single line & we discussed this for 3/4 too....

And then also drew their attention to where they were stuck earlier.. To this one of them quickly said -

"It will be 0.875"

"And How?"

"I see that the decimal point in the Numerator goes away when there is one more zero in the Denominator"

The other student also confirmed this observation. I asked them to check this with the answer they have got using std. method of multiplication. And they were highly delighted to see that it matched (1.875)

A thought came to me for a while, (based on the way student had seen and explained) that I should now ask them what would happen (how would they write in decimal form), if it were 8.75 / 100 or say 13.25 / 100 or 4.26 / 10

(why such doubts came to teacher's mind? and share your thoughts about the 3 questions made?)

But then I chose to & even we had to pause this discussion here for some reasons.... So while they were now about to happily leave (after this adventure), I drew their attention to the problem which led us to all this exploration & discoveries....

"What's the value of square root of 3 ?"

And they started laughing :)

"So Is it 1.5?"

"No"

"So then what would it be ?"

"It will be between 1.5 and 2"

"How do you know ?"

"Because we saw that 1.5 squared is 2.25 and 2 squared is 4."

"So this is your home-work now to find the value of square root of 3"

And they left happily agreeing to this challenge :)

-----------------------

Day-2

I asked them if they could get the value...

And what do you think could have happened? Will probably share this in the following post :-)

Thanks and Regards

Rupesh Gesota

www.rupeshgesota.weebly.com