Plan was to help them see the relationships between the side lengths in 30-60-90 Triangles. But without hinting this to them, I told them to Construct couple of Right angled triangles in their note-books having other angles as 30 and 60 and with lengths of their hypotenuse as 10 cm and 6 cm
Then I told them to measure & tell me the other 4 side lengths in both triangles. I wrote these on the board as above and then asked them - What do they Notice? They were quick to see and say that
"in both the triangles, the shortest side length is always half the longest one"
I told them to construct two more Right Triangles, with hypotenuse as some whole numbers, but with angles other than 30 & 60 this time. They observed that in these cases shortest is Not half of the longest. So they said this relation holds true only when the angles are 30-60-90. (Can the need & timing of this 2nd activity be justified?)
So now I drew the following figure on the board and asked them if they could find which side length would be half of the hypotenuse length, without actually constructing it. (what could be the reason for doing this activity? Isn't this a mere repetition of the very first activity?)
Now It took some time for them to figure out. But after carefully studying previous figures, they said that "Side opp. to 30 degrees will be half of the hypotenuse"
So now, I asked them - If there could be any relation between the side opp. to 60 degrees angle and hypotenuse?
Their side lengths were in decimals (5.1 and 8.7), so it was naturally difficult for them to easily relate those to hypotenuse lengths. I asked them if they know any theorem that can be used in Right Angled Triangles. And they immediately said - Pythagoras theorem. And so we applied it & finally reached till this step.
Only last part of the derivation is showed above. A right angled Triangle was drawn where Hypotenuse was 'x', side opp. to 30 degrees angle = x/2 and side opposite to 60 degrees angle was shown as 'y'. Each of these steps were told by them and just written by me. I asked them how did they arrive at (1.5 x / 2) and they said
"Square root of x^2 = x , square root of 4 is 2 and sq. root of 3 is 1.5"
Suggesting you to Pause and think how would you respond at this moment?
...
...
...
...
...
...
...
...
...
...
"Okay... And how do you know that sq. root of 3 is 1.5?"
"Sq. roots of 1 and 4 are 1 and 2 resp. So sq. root of 3 has to be between 1 and 2.. So it should be 1.5"
Before reading further, I suggest you to pause and think for a while as to what would you do at this moment ?
...
...
...
...
...
...
...
...
...
I asked them if they can verify it. They started multiplying 1.5 by 1.5 using standard procedure. I would have loved seeing them figure out this product mentally through reasoning (Can YOU try that way before reading further?) And I thought we will discuss this approach once they get the answer using std. method, but then something else happened (& now I was in fact glad that they went by the std. multiplying method :-)
They seemed puzzled / uncomfortable with their results. So I told them to show their work on the board.
"What's the problem?"
"Both answers are incorrect as they are greater than 4. Because the product : 1.5 times 1.5 has to be between 1 and 4."
"Okay... But then how come both of you have got different results?"
So then they started comparing / studying each other's methods. And one of them tried this:
"But then this is also incorrect. It is less than 1", he said
"Okay... So what to do now? How to find what's 1.5 x 1.5?" I asked. They looked more engaged / puzzled than earlier now. I waited for about half a minute. After that, I decided to intervene. (Share your comments about this paragraph (approach by the teacher)
And before reading further, I suggest you to pause and think for a while as to what would you do at this moment ?
....
.....
....
....
....
....
....
....
....
There can be many ways. This is what happened through me at that moment:
"What's the other way we can write 0.5?" (when can a teacher help by asking such a question?)
And they picked up the hint and did this:
They reasoned out for 6/4 as if 6 chapatis given to 4 people, then each gets one and half, so 6/4 = 1.5 and 1/4 = 0.25 because 1 rupee = 100 paise, so quarter means 25 paise.
They were delighted with this answer 2.25 because it satisfied their expectation that it needs to be between 1 and 4. Further the boy who had worked out 1.5 x 1.5 as 0.225 on the board, something clicked to him; he went and corrected his answer -
"I had placed the decimal point incorrectly"
"But then how would you know where to place the decimal point?"
He studied the work again, and said, "Count the number of digits after the decimal point in both the numbers, add them, & then place it accordingly in the product."
"Okay.. It seems you have made a Rule. Will this always work?"
"Sir let's take one more example." And they did this:

"Okay... but what if there is 1 digit after the dp in 1st no. and 2 digits after the dp in 2nd no. ?"
"Then we will put the dp after 3 digits in the product."
"Will that work?"
"We will take an example to check." And they did this :
((( I would like to share something interesting that happened when they were framing the example for this case... One of them selected the numbers as 11.5 and 1.5 Why do you think he took such numbers?
I would have loved to see the story that can unfold after testing with 11.5 and 1.5, but since both of them were working together, so the other boy noticed this and he corrected him explaining what rule they are testing... Later I felt, I could have even suggested this boy to continue his testing independently with 11.5 & 1.5 .... )))
So now they were stuck with another problem: How to write 7/8 in decimal form?
They had been using 1 rupee = 100 paise, 1/2 rupee as 0.5 and 1/4 = 0.25 till now. So now they were struggling for 7/8.... For a while, they suggested 0.12.5 for 1/8 (Can you reason out why they must have said so?) But then they said they were uncomfortable with this because they had never seen such notation till now. After a while, they got stabilised at following:
They noticed that the digits (8,7 and 5) in this new representation were same as the ones they had got by multiplying 1.5 and 1.25 using standard method. But the different positions of decimal points in these two representations was bothering them.
Suggesting you to Pause here and Think about your approach now..
...
...
...
...
...
...
...
...
...
"Okay, so you have been dividing the whole into 100 parts to find the digits after the decimal point, right?"
"Yes.. because 1 rupee = 100 paise"
"Do these numbers represent always Money?"
"No"
But this hint did not help them... They were still stuck...
Suggesting you to Pause here & Think about your approach at this moment...
...
...
...
...
...
...
...
...
...
...
...
"How do you write half?"
1/2
"And using decimal point ?"
0.5
"How do you get this 5 in 0.5? Why not 0.2 , 0.3 ?"
We can write 1/2 as 5/10 and Out of 10 parts, we have taken 5 parts... So 0.5
"Okay... So you have converted 1/2 into other form 5/10 to find the decimal point form of half ? "
Yes
"But then why not write 1/2 as 3/6 and then write half as 0.3 ? Or write 1/2 as 4/8 and write half as 0.4 ?"
No answer. Puzzled.
"You have been dividing the whole into 100 parts till now to get the digits after the decimal point... So how will you write half in such case ?"
They said : 50/100 which is 0.50
"So do 0.5 and 0.50 both mean half ? "
Yes
"Which one is greater?"
Both are equal. 5/ 10 can be written as 50/100
"What about 0.500 ?"
This is also same ... Here we have done 500/1000
I thought this discussion might help them to think, go back and divide their whole into 1000 parts now instead of 100 which they had done because of which they had got decimal point number in the Numerator (87.5) and they felt stuck... But probably this much discussion didn't click much to them either... So then I asked -
"How do you write 1/4 using decimal point ?"
0.25
"How do you get this ?"
25/100
"Can we divide here too into 10 parts as we had done with half ?"
Yes. It would then be 2.5 / 10
"So which of these mean quarter ?"
All of these.
So I now wrote all of these in a single line & we discussed this for 3/4 too....
And then also drew their attention to where they were stuck earlier.. To this one of them quickly said -
"It will be 0.875"
"And How?"
"I see that the decimal point in the Numerator goes away when there is one more zero in the Denominator"
The other student also confirmed this observation. I asked them to check this with the answer they have got using std. method of multiplication. And they were highly delighted to see that it matched (1.875)
A thought came to me for a while, (based on the way student had seen and explained) that I should now ask them what would happen (how would they write in decimal form), if it were 8.75 / 100 or say 13.25 / 100 or 4.26 / 10
But then I chose to & even we had to pause this discussion here for some reasons.... So while they were now about to happily leave (after this adventure), I drew their attention to the problem which led us to all this exploration & discoveries....
"What's the value of square root of 3 ?"
And they started laughing :)
"So Is it 1.5?"
"No"
"So then what would it be ?"
"It will be between 1.5 and 2"
"How do you know ?"
"Because we saw that 1.5 squared is 2.25 and 2 squared is 4."
"So this is your home-work now to find the value of square root of 3"
And they left happily agreeing to this challenge :)
-----------------------
Day-2
I asked them if they could get the value...
And what do you think could have happened? Will probably share this in the following post :-)
Thanks and Regards
Rupesh Gesota




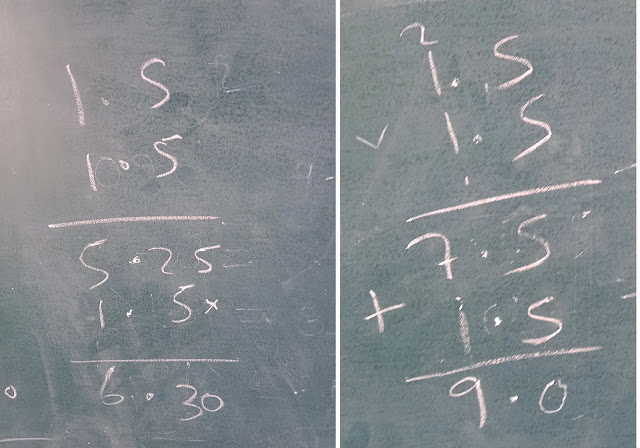










No comments:
Post a Comment